Sample Size for a Moderated Mediation:
Using G*Power
How to calculate the necessary sample size for a moderated mediation with PROCESS (model templates 7, 8, 14, 15).
Arndt Regorz, Dipl. Kfm. & M.Sc. Psychologie, 31/10/2024
This tutorial will show you how to use the free software G*Power to plan your sample size for a moderated mediation with Hayes’ Process macro
Introduction
If you want to test a moderated mediation model, e.g. model 7, model 8, model 14, or model 15 with PROCESS for SPSS or for R, then you should plan the necessary sample size.
However, there are not many good tools for power calculation for a moderated mediation. One easy way to get a rough estimate about the sample size you need to find your effects is using the free software G*Power.
When we are talking about statistical power in any context the crucial question is: For what specific effect do you want to calculate the power?
In a moderated mediation the key measure is the index of moderated mediation. In models 7 and 8 that is the product of the regression weight for the interaction for the a-path and the regression weight for the b-path. In models 14 and 15 it is the product of the weight for the a-path and the weight for the interaction for the b-path.
If this index of moderated mediation is significant, then you have a moderated mediation.
If this index is not significant, then you don't have a moderated mediation.
With G*Power you can't calculate the exact power for this product of to regression weights. But what you can do is this: You can perform a power calculation for the two components of the index of moderated mediation, that is for the interaction for the one path and for the other path. The question then is: How large a sample size do you need in order to have a power of, e.g., .80, for both effects that go into the index of moderated mediation to be significant at the same time?
Let me show you how to do that, starting with model 7.
Using G*Power to Calculate the Power for Model 7
First, you have to identify the regression models that go into the PROCESS model you want to test.
Let's assume you want to run PROCESS model 7, the conceptual diagram of this model is here:
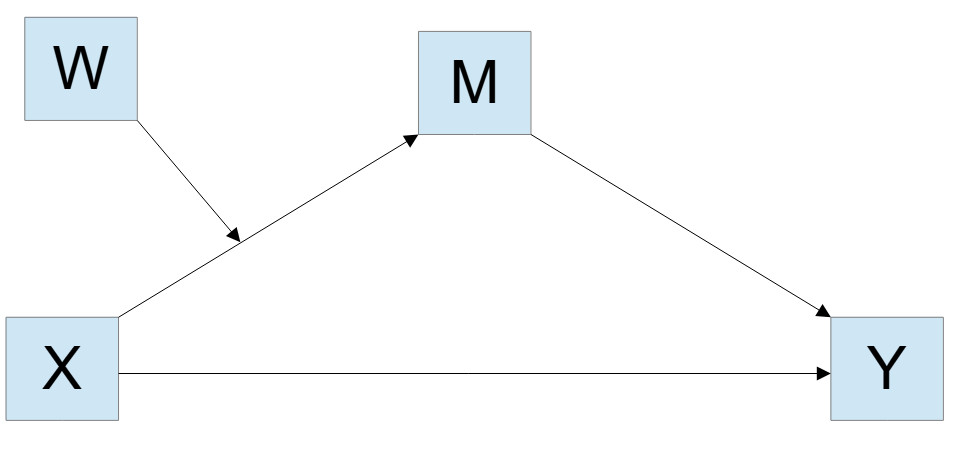
This is the statistical diagram for the same model:
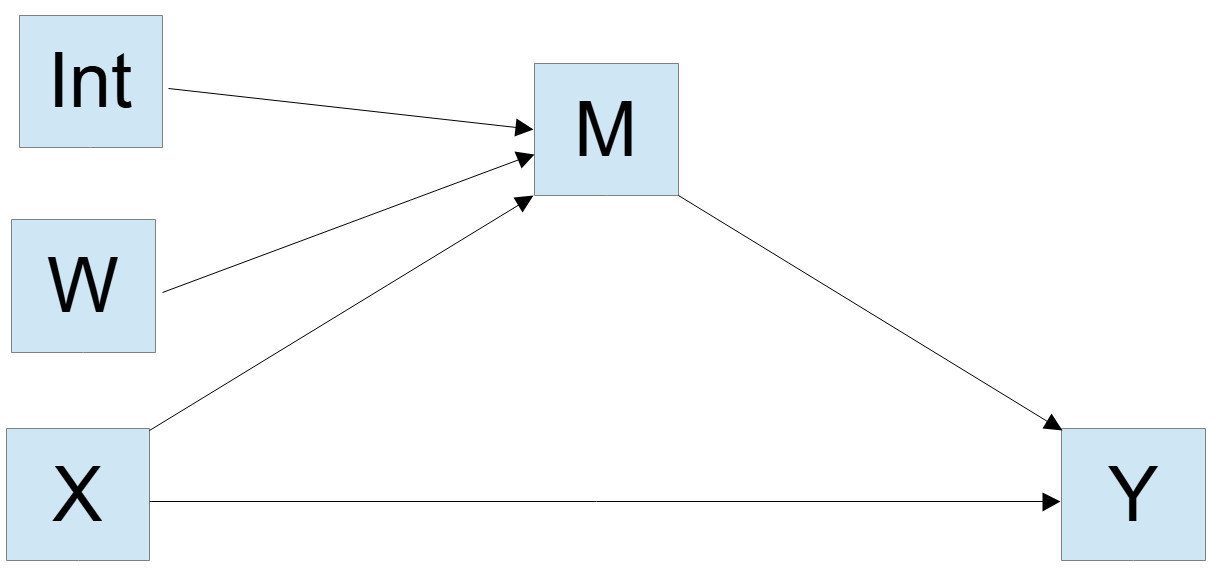
You have two regression models, one for predicting the mediator and one for predicting the dependent variable.
Both are multiple regressions, and you can use G*Power for calculating the sample size for a multiple regression.
But it is a little bit more complicated because now you are interested in the probability of both effects being significant at the same time. You will see later how you can deal with this problem.
In order to perform any power analysis, you need an assumption about the size of the effect you want to find. In this case you need two assumptions:
How large is the effect for the interaction of the a-path?
How large is the effect for the b-path?
Ideally, you can base that on earlier research in the literature. Otherwise, you will have to make some general assumptions about the effect sizes (small, medium, large).
G*Power works with Cohen's f² as an effect size measure for a multiple regression:
- 0.35 would be a large effect
- 0.15 a medium effect
- 0.02 a small effect
But of course you can also assume an effect size in between those numbers, e.g., an effect size halfway between small and medium.
In this tutorial we will look at three possible cases and how to perform the power calculation for those:
- Both effects sizes are extremely different
- Both effect sizes are somewhat different
- Both effect sizes are the same
1. Extremely Different Effect Sizes
Let's assume you expect a medium sized effect for the b-path (0.15) but only a small effect for the interaction of the a-path (0.02).
You always start with the smaller effect because that is the bottleneck.
Here are the input values for G*Power for the first regression model (interaction of the a-path) which has in this example the smaller of the two effects:
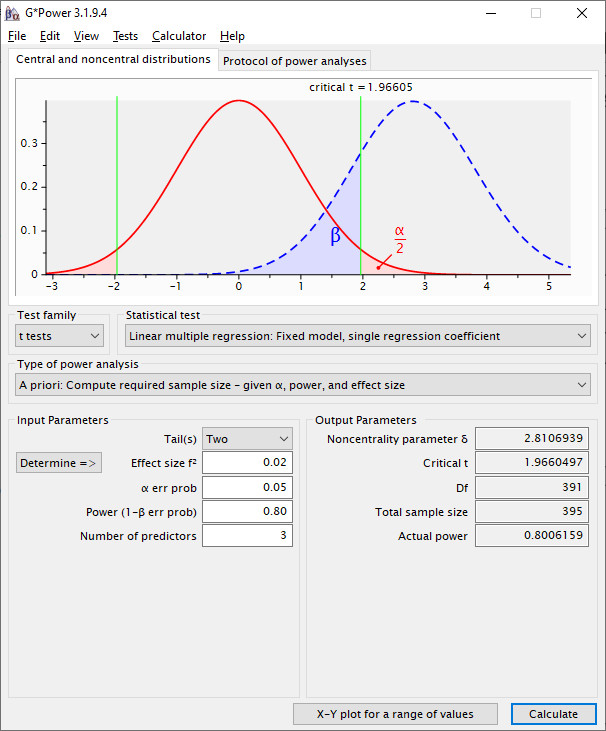
You can see the number of predictors in the statistical graph for model 7. There are three predictors predicting the mediator (IV, moderator, interaction).
As a result you get a sample size of 395 to find a significant interaction for the a-path.
However, you want to be able to find a significant b-path at the same time.
Let's see how large the power is for the b-path with this sample size of 395. For this you run a post-hoc power analysis with this sample size and the assumed effect size for the b-path, using these input variables (number of predictors is 2 here, see the diagram for model 7):
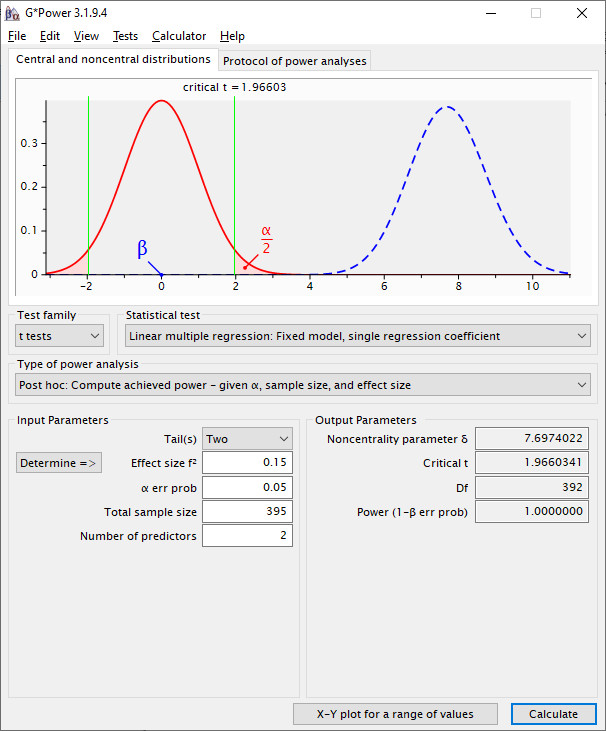
In this case the power for the b-path is 1.00.
Assuming both effects are statistically independent you can calculate the power for both effects to be significant at the same time by multiplying the two power values.
Interaction a-path: .80
B-path: 1.00
Overall power: .80 x 1.00 = .80
Thus, in this case you need a sample size of 395 for the moderated mediation to get to a power of .80 for detecting both effects at the same time.
You can see that with very different effect sizes only the smaller effect matters for the sample size.
But that is not the case if both effects are only moderately different. That will be the next case we are going to look at.
2. Somewhat Different Effect Sizes
Let's assume you expect a medium sized effect for the b-path (0.15) but this time an effect for the interaction of the a-path that is halfway between small and medium, e.g., 0.085.
Again, you start with the smaller effect, using these input values:
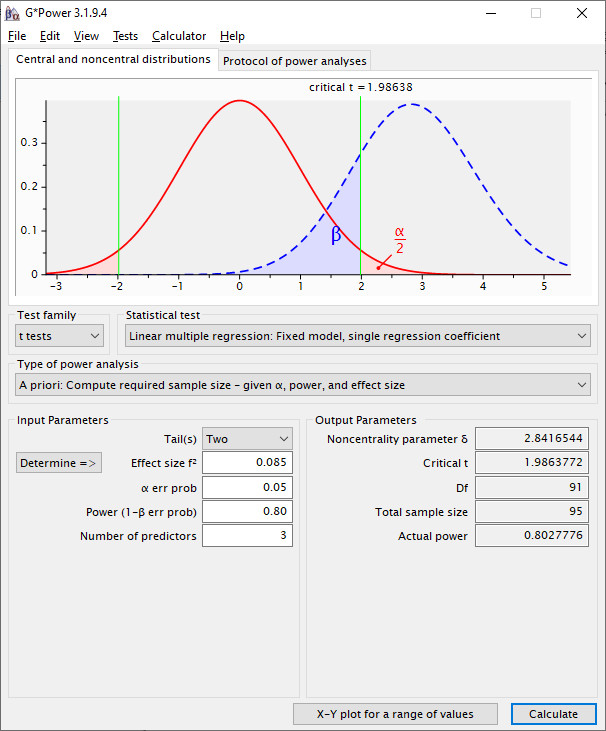
Here, you need 95 for the interaction for the a-path alone.
Next, calculating the post-hoc power for the b-path with this sample size and the assumed effect size for the b-path:
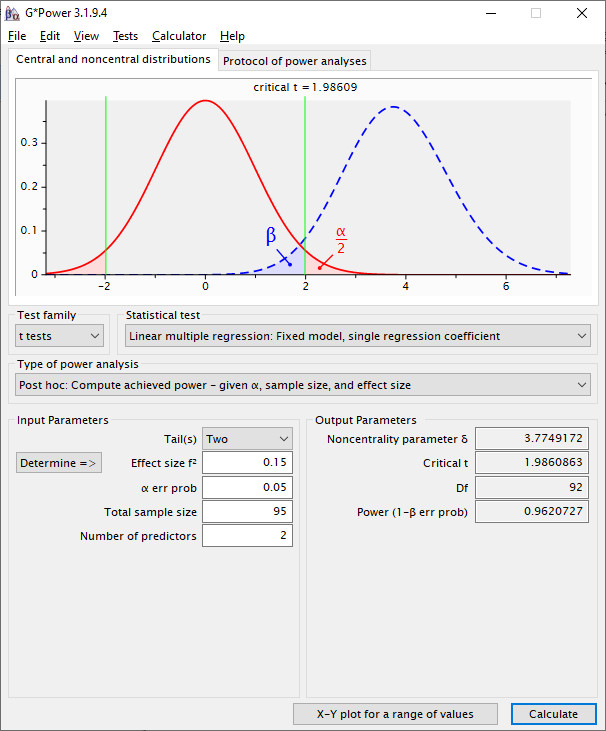
Here you get a power for the b-path of .962.
The overall power for detecting both effects, assuming independence of both effects, is:
.80 x .962 = .7696
That is below the threshold of .80 you wanted to achieve.
For that reason you have to increase the power for testing the interaction so there is something left for the b-path.
Since the power for the b-path was about .96, that is .04 smaller than 1, I would add a little bit less than that difference to the power of .80 for the interaction of the a-path, to let's say a power of .83 for the interaction. With this new power for the a-path you repeat the calculation:
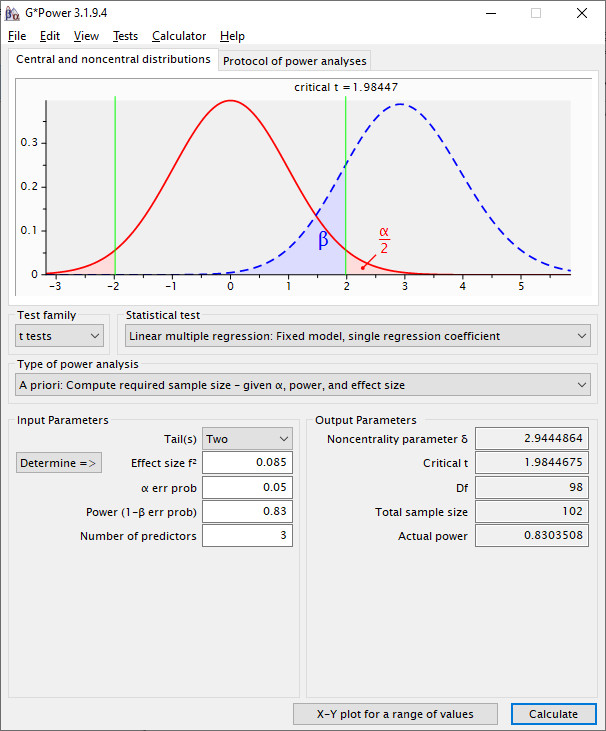
This results in a sample size of 102.
Again, you run the post-hoc power analysis for the b-path with this sample size:
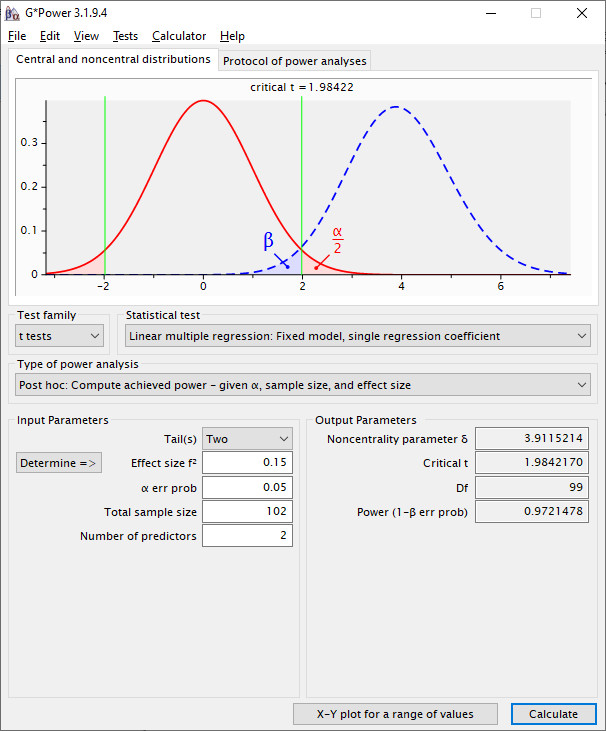
The resulting power for the b-path is .972.
From that you can calculate the overall power for detecting both effects at the same time (assuming independence for both effects):
.83 x .972 = .807.
(If this power of .807 seems too high for you, then you could repeat the calculation a third time, this time for example with a power of .8275 for the interaction, to get even nearer to a power of .800.)
This is above our threshold of .80, thus, here 102 cases are sufficient.
Next to the case of two equal effect sizes for the interaction and for the b-path.
3. Same Effect Sizes
Let's assume you expect effects halfway between small and medium, e.g., 0.85, for both the interaction for the a-path and for the b-path.
In this case the calculation gets easier. If you want to get an overall power of .80, then you simply need a power for both effects of the square root of .80 each, sqrt(.80) = .8944. Because then the overall power is:
.8944 x .8944 = .80
Here is the G*Power input for the interaction for the a-path (with 3 predictors):
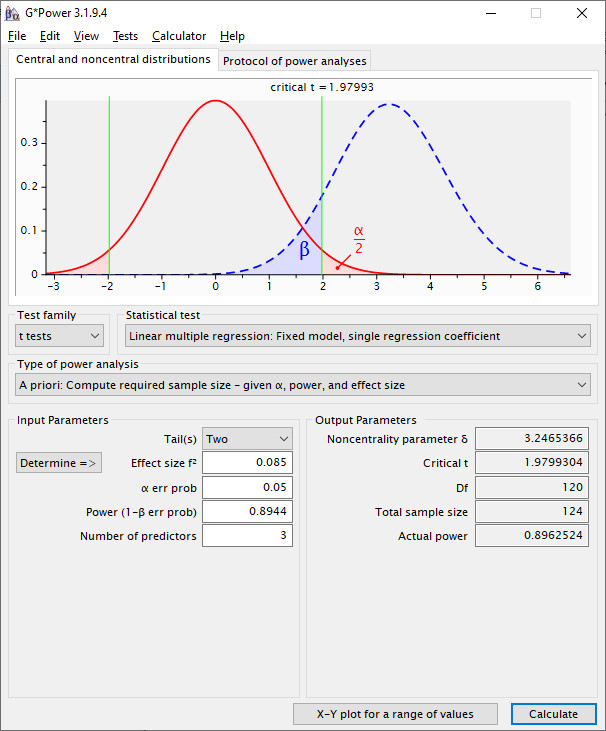
This results in a sample size of 124.
Here is the input for the b-path (with 2 predictors):
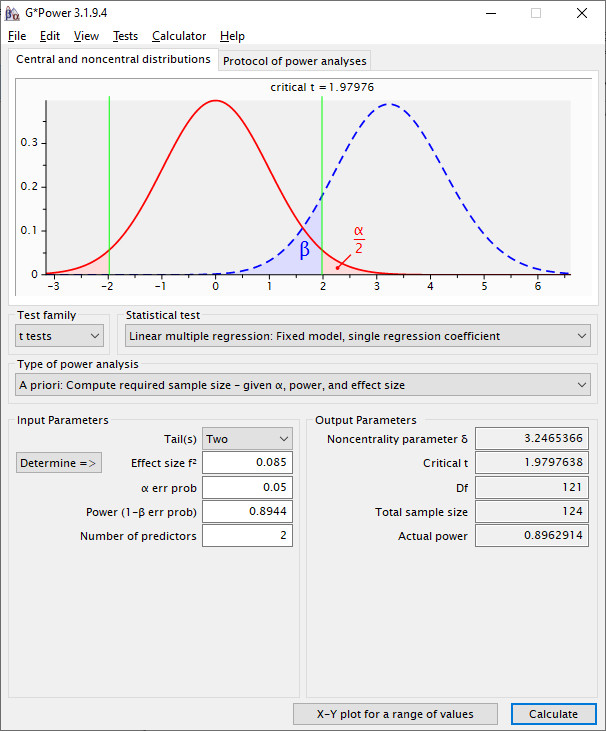
Again, you get a sample size of 124.
Thus, in this case you need a sample size of 124 to achieve a power of .80.
Other PROCESS Models
Up to now I have shown you how to calculate the power for process model 7, but the same logic applies to models 8, 14 and 15.
The only difference is that the number of predictors you have to use in G*Power is different
(and of course that for models 14 and 15 you test the a-path and the interaction of the b-path).
In PROCESS model 8 you have 3 predictors for the first model (predicting the mediator) and 4 predictors for the second model (predicting the dependent variable).
In PROCESS model 14 you have 1 predictor for the first model and 4 predictors for the second model.
In PROCESS model 15 you have 1 predictor for the first model and 5 predictors for the second model.
If you plan to have covariates in your model, then you have to add the number of covariates to the numbers above. But one or two covariates won't change much for the results of your calculations (however they might change the effect sizes you should expect).
Limitations
There are some limitations to this approach you should know, because there are two somewhat simplifying assumptions that go into this calculation
The first assumption is that the power for the index of moderated mediation is equivalent to the power for both components being significant at the same time, and that isn't exactly true. With PROCESS the index is calculated by using bootstrapping. It is possible that the index of moderated mediation is significant, but that one of the components is not. The opposite is possible, too: Both components can be significant, but the index of moderated mediation is not. However, I believe those cases are quite rare.
The second assumption is that both parts (in model 7 the interaction for the a-path and the b-path) are statistically independent. Only then can we calculate the overall power by multiplying the power of both components.
For those reasons the results are only an approximation of the needed sample size, not the exact value. But I do think this approach gives you a reasonable estimate.
Nevertheless, it can be a good idea to add some margin of safety to the resulting number, e.g. adding 10% to the results of the power calculation.
Reporting
Here is a possible example of how to report your sample size calculation. In the case of two somewhat different effect sizes (the second case from above) I would report the final calculation:
The sample size for the moderated mediation was planned using the software G*Power (version ……).
As a plausible effect size for the interaction of the a-path an f² of 0.085 was assumed, for the b-path an f² of 0.15. These effect sizes are based on ….. [and here you will have to insert your reasons or sources from which you have deduced these values]
For the interaction of the a-path a power of .83 for a two-tailed test of a single regression coefficient (with alpha = .05 and three predictors in the submodel) resulted in a sample size of 102. Using the same sample size of 102 in a power calculation for the b-path (two-tailed, alpha = .05, two predictors in the submodel) lead to a power of .972 for the assumed effect.
This resulted in an overall expected power of .83 x .972 = .807, assuming statistical independence of both effects. Thus, a sample size of 102 can be seen as sufficient to achieve a statistical power of at least .80 for testing that both parts of the moderated mediation are significant at the same time.
Since there were simplifying assumptions involved in this power calculation (e.g., independence of both effects, not using bootstrapping), 10% was added to the sample size of 102 as a margin of error, resulting in a planned sample size of 113 participants.
Possible Alternatives
There are a couple of alternatives to calculate the power of a moderated mediation in the form of R packages. However, none of those is convincing for me. Either it is quite difficult to derive the correct input values, or the module is difficult to use, or it does not give you a power value for the index of moderated mediation (and that is what counts).
But for completeness sake, here are three possible alternatives you could look into: