Pfadanalyse mit Mplus:
Einführung

Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, 21.02.2023

Mplus ist ein sehr mächtiges SEM-Programm (CFA, SEM, path models). Dieses Tutorial zeigt an einem einfachen Beispiel, wie man mit Mplus ein Pfadmodell testen kann.

Inhalt

1. Video-Tutorial
2. Grundlagen Mplus-Syntax
3. Modellspezifikation (model specification)
4. Modellschätzung (model estimation) und Modelevaluation (model evaluation)
5. Modellrespezifikation (model respecification)
6. Modellinterpretation (model interpretation)
7. Quellen

1. Video zur Pfadanalyse mit Mplus

(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)

2. Grundlagen Mplus-Syntax

Mplus ist ein skriptorientiertes Programm: Man legt ein neues Skript an und schreibt in dieses Skript die Befehle für die Pfadmodellierung. Anders als bei anderen Statistikprogrammen hat man zu diesem Zeitpunkt noch gar keine Daten im Hauptspeicher, diese werden erst durch das Skript in den Speicher des Computers geladen.

Hier ist ein Beispielskript für ein Pfadmodell, an dem man einige Grundlagen von Mplus gut verdeutlichen kann:

TITLE:
Modell 1
Erstes Pfadmodell ohne direkte Effekte;

DATA:
FILE IS simulationsdaten_pfadanalyse.csv;

VARIABLE:
NAMES ARE lfdnr uv1 uv2 med av1 av2;
USEVARIABLES ARE uv1 uv2 med av1 av2;
MISSING IS all (-99);

MODEL:
med ON uv1 uv2;
av1 ON med;
av2 ON med;
av1 WITH av2;
uv1 WITH uv2;

OUTPUT:
MODINDICES(15); ! Die (15) bedeutet, dass nur MIs > 15 ausgegeben werden
STDYX;
CINTERVAL;

Das Skript ist gegliedert in Abschnitte, hier im Beispiel sind es fünf (TITLE, DATA, VARIABLE, MODEL, OUTPUT) – je nach gewählter Modellierung können es aber auch mehr oder weniger sein. Nach jedem Abschnittsnamen steht ein Doppelpunkt.

Unterhalb der Abschnitte sind die Mplus-Befehle aufgeführt. Diese enden jeweils mit einem Semikolon. Eine Befehlszeile darf bis zu 90 Zeichen lang sein – wenn sie länger ist, muss eine neue Zeile begonnen werden. Mplus unterscheidet nicht zwischen Groß- und Kleinbuchstaben. Ich habe mir angewöhnt, dass ich Befehle groß schreibe und meine eigenen Variablennamen klein, um so die Lesbarkeit zu erleichtern – aber das ist ausdrücklich Geschmackssache. Kommen wir jetzt zu den einzelnen Abschnitten.

Der Abschnitt TITLE besteht nur aus dem Titel selbst, in dem man mehr oder weniger ausführlich beschreibt, was die jeweilige Auswertung bedeutet. Dies erleichtert später die Lesbarkeit des Codes für Sie oder andere.

Im Abschnitt DATA wird der Datenimport geregelt. Mit dem Kommando FILE IS wird vorgegeben, welche Datendatei Mplus laden soll. Hier im Beispiel wird eine csv-Datei geladen, aber Mplus kann auch andere Datenformate lesen, z.B. dat-Dateien (die Sie beispielsweise beim Export von SPSS nutzen könnten). Falls die Datendatei im gleichen Verzeichnis steht wie die Skriptdatei, dann reicht hier die Angabe des Dateinamens. Falls jedoch die Datendatei in einem anderen Verzeichnis stehen sollte, müssen Sie den vollständigen Dateipfad angeben, damit das Programm die Datei finden kann.

Bei der Datendatei gibt es noch eine Besonderheit, die man so von so gut wie keinem anderen Programm kennt: Die Datendatei ist eine Datei ohne Spaltenbeschriftungen (Variablennamen). Also bereits die erste Zeile der Datendatei ist schon der erste Datensatz – man kann also aus der Datendatei nicht erkennen, welche Zahlen überhaupt was bedeuten. Woher weiß Mplus dann, welche Zahlen zu welcher Variable gehören? Das wird im nächsten Abschnitt geklärt.

Im Abschnitt VARIABLE werden wesentliche Informationen über die zu verarbeitenden Daten gegeben. Zunächst wird mit dem Befehl NAMES ARE spezifiziert, welche Spalte in der Datendatei welchen Variablennamen trägt. Dabei wird einfach jeder Spalte von links nach rechts ein Name gegeben. Mit USEVARIABLES ARE wird angezeigt, welche Variablen in Ihrem Pfadmodell verwendet werden (häufig verwendet man nur einen Teil der Daten eines Datensatzes als Variablen im Pfadmodell). Und mit MISSING IS wird spezifiziert, welche Werte Anzeichen für fehlende Werte (missing values) sind und als solche, und nicht als Zahl, zu behandeln sind.

Der Abschnitt MODEL ist die eigentliche Modellspezifizierung. Auf diese wird im nächsten Abschnitt ausführlicher eingegangen.

Und im Abschnitt OUTPUT kann man zusätzliche Ausgabeinfos anfordern. In diesem Beispiel sind das mit MODINDICES(15) Modifikationsindizes – hier nur diejenigen, die größer als 15 sind, mit STDYX standardisierte Ergebnisse („betas“) zusätzlich zu den unstandardisierten Ergebnissen und mit CIINTERVAL Konfidenzintervalle für die zu schätzenden Parameter.

Außerdem sieht man hier noch, wie man in Mplus Kommentare einfügen kann. Diese werden mit einem Ausrufungszeichen gekennzeichnet - alles, was danach in der gleichen Zeile erscheint, wird von Mplus nicht verarbeitet.

3. Modellspezifikation (model specification)

Der Kern jedes Mplus-Skripts ist die Modellspezifikation, also die Angabe, was für ein Zusammenhang zwischen den Modellvariablen getestet werden soll.

Wir möchten beispielsweise dieses Pfadmodell testen:

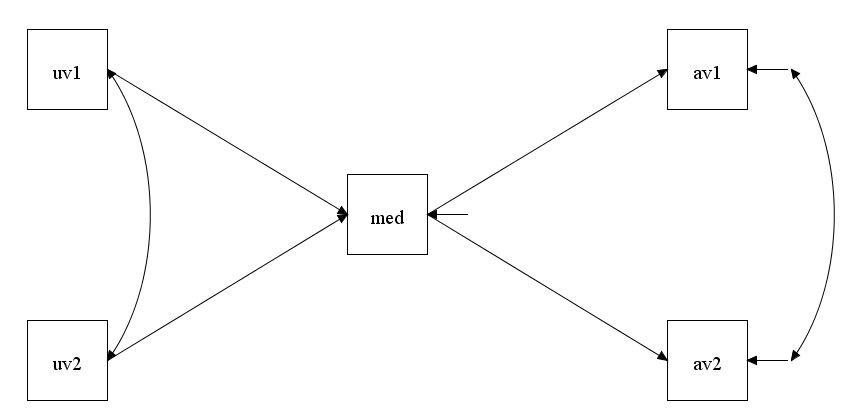
Wir haben also zwei unabhängige Variablen, einen Mediator und zwei abhängige Variablen. Und die Fehlerterme der abhängigen Variablen sollen miteinander kovariieren/korrelieren (auch die Fehlerterme der unabhängigen Variablen, aber dort ist es eigentlich immer Standard, dass man eine Kovarianz annimmt).

Hier ist nochmals der Code für die Modellspezifikation angegeben:

MODEL:
med ON uv1 uv2;
av1 ON med;
av2 ON med;
av1 WITH av2;
uv1 WITH uv2;

Zunächst müssen wir die im Modell enthaltenen Disturbances (Fehlerterme) der endogenen Variablen (Mediatoren, abhängige Variablen) nicht explizit modellieren, das übernimmt Mplus für uns. Damit bleiben in der Modellgrafik zwei Arten von zu modellierenden Zusammenhängen: Gerichtete einfache Pfeile (Regressionspfade) und ungerichtete Doppelpfeile (Kovarianzen).

Die gerichteten Regressionspfade werden mit dem Schlüsselwort ON definiert. Das kommt aus dem englischen, wo man sagt, die abhängige Variable wird „regressed on“ die unabhängigen Variablen. Die Zeile „med ON uv1 uv2;“ bedeutet also, dass die Variable med vorhergesagt wird von den beiden Prädiktoren uv1 und uv2.

Die ungerichteten Kovarianzen werden mit dem Schlüsselwort WITH definiert, das kommt von „covaries with“. Die Zeile „av1 WITH av2;“ besagt also, dass eine Kovarianz zwischen diesen beiden Variablen (bzw. hier genauer zwischen deren Disturbances) geschätzt werden soll.

In der Literatur schließt sich an die model specification häufig noch der Schritt der model identification an, also die Prüfung, ob das Modell überhaupt theoretisch schätzbar ist. Allerdings ist das bei Pfadmodellen im Vergleich zu CFAs und vollen SEM-Modellen in der Regel ein geringeres Problem. Insbesondere dann sollte man keine Schwierigkeiten bekommen, wenn man einerseits zwischen zwei Variablen nur maximal eine Verbindung (Pfad a zu b, Pfad b zu a, oder Korrelation a mit b) schätzt und andererseits keine Kreisläufe in den Daten hat (also nicht Pfeile von a auf b, b auf c, und dann c wiederum zurück auf a).

Was häufiger bei Pfadmodellen vorkommen kann ist, dass man am Ende ein saturiertes Modell hat, also ein Modell mit 0 Freiheitsgraden. Wenn das bei Ihnen der Fall ist, können Sie hier meine Einschätzung dazu sehen, warum das kein grundsätzliches Problem ist: Pfadanalyse mit 0 Freiheitsgraden.

4. Modellschätzung (model estimation) und Modelevaluation (model evaluation)

Das Modell wird dann geschätzt, indem man in der Symbolleiste oben in Mplus auf die Schaltfläche „RUN“ klickt. Als Ergebnis erhält man jetzt eine Outputdatei, auf deren wichtigste Elemente im Folgenden eingegangen wird.

Zunächst erhält man unter INPUT INSTRUCTIONS nochmals den Inhalt des eigenen Befehlscodes. Idealerweise folgt die Ausgabe INPUT READING TERMINATED NORMALLY, die anzeigt, dass die Daten erfolgreich gelesen werden konnten. Bei den anschließenden Vorauswertungen sind insbesondere die UNIVARIATE SAMPLE STATISTICS relevant.

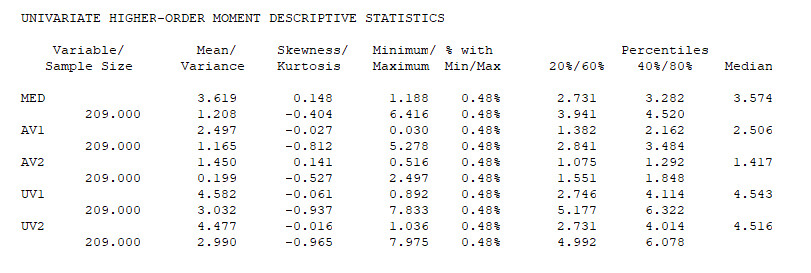
Bei Mplus ist eine Fehlerquelle der Datenimport bzw. die Zuordnung der Variablennamen zu den verschiedenen Spalten. Um sicherzustellen, dass man dort keinen Fehler gemacht hat (z.B. durch Vertauschen von zwei Spaltennamen oder durch Vergessen eines Spaltennamens), empfehle ich, Mittelwert und Varianz aus dieser Auswertung mit einer entsprechenden deskriptiven Auswertungen desjenigen Statistikprogramms abzugleichen (z.B. SPSS, R, usw.), aus dem Sie die Daten exportiert haben. Wenn die deskriptiven Auswertungen zum gleichen Ergebnis führen, dann ist das in der Regel ein gutes Indiz für einen fehlerfreien Import der Daten.

Daran anschließend betrachtet man die Informationen zum eigentlichen Model-Fit.

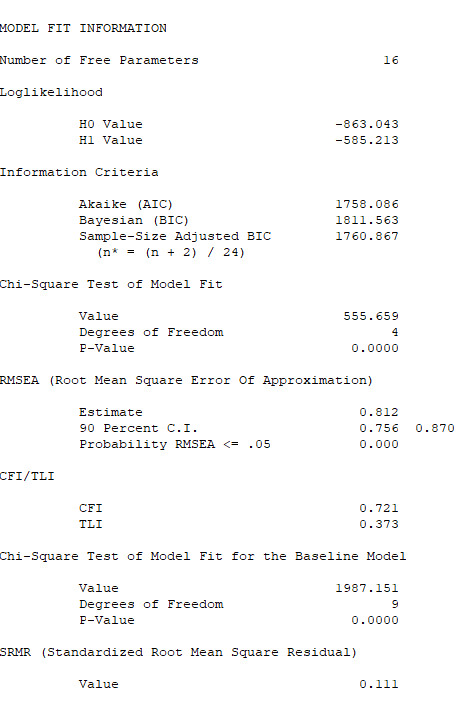
Zunächst ist es wichtig, dass die Zeile THE MODEL ESTIMATION TERMINATED NORMALLY erscheint, dass das Programm also eine stabile Schätzung für das Modell durchführen konnte.

Anschließend betrachtet man den Modelltest (Chi-Quadrat-Test) auf exakten Modellfit sowie mehrere Fit-Indizes (ich verwende vor allem CFI, RMSEA und SRMR).

Der Modelltest (Chi-Square Test of Model Fit) ist hier mit einer Teststatistik von 555.659 bei 4 Freiheitsgraden hoch signifikant mit p < .001. Das Modell passt also nicht perfekt zu den Daten, aber das tut es fast nie.

Daher betrachten wir als nächstes die Fit-Indizes. Der RMSEA ist bei Modellen mit nur sehr wenigen Freiheitsgraden nicht sinnvoll interpretierbar (siehe Probleme mit dem RMSEA bei wenigen Freiheitsgraden), insofern können wir uns hier auf CFI und SRMR stützen. Der CFI mit .721 liegt deutlich unter dem empfohlenen Cut-Off-Wert von .95 (Hu & Bentler, 1999). Auch der SRMR mit .111 liegt über dem Cut-Off-Wert von .08.

Insgesamt haben wir hier also einen schlechten Modellfit. Daher können wir die weiteren Ergebnisse der Modellschätzung nicht sinnvoll interpretieren, da sie bei einem Modell mit schlechtem Modell-Fit stark verzerrt sein können.

5. Modellrespezifikation (model respecification)

Da das Modell nicht hinreichend gut zu den Daten gepasst hat, was wir am schlechten Modell-Fit ablesen konnten, geht es jetzt um die Veränderung des Modells. Dafür nutzt man Modifikationsindizes, die anzeigen, welche zusätzlich frei zu schätzenden Parameter zu einem bessere Modell-Fit führen können.

Beim Einsatz von Modifikationsindizes sind zwei Punkte wichtig: Zum einen sollte man auf keinen Fall einfach blind die Veränderung mit dem höchsten Modifikationsindex (und damit mit der höchsten zu erwartenden rechnerischen Modellverbesserung) vornehmen. Stattdessen sollte man diejenige Veränderung mit hohem Modifikationsindex vornehmen, die theoretisch gut begründbar ist. Zum anderen sollte man in der Regel nur eine einzige Änderung zur Zeit vornehmen, weil eine Änderung häufig mehrere Probleme im Modell-Fit zugleich beseitigt – denn in Pfadmodellen zeigen sich Fit-Probleme häufig an verschiedenen Stellen, nicht nur an der Stelle der eigentlichen Ursache.

Hier ist der Output der Modifikationsindizes für das Beispielmodell (wie angefordert begrenzt auf Indizes über 15):

Wir sehen sowohl vorgeschlagene zusätzliche Regressionspfade (ON statements) als auch zusätzliche Kovarianzen (WITH statements). Die beiden größten Modifikationsindizes sind zum einen für AV1 ON UV1, also ein zusätzlicher direkter Effekt von der UV1 auf die AV1, die bisher nur durch einen indirekten Effekt über den Mediator verbunden sind. Zum anderen UV1 WITH AV1, also eine Kovarianz zwischen der UV1 und der Disturbance von AV1 – das ist jedoch theoretisch kaum begründbar und interpretierbar.

Insofern ändern wir jetzt unser Modell dahingehend, dass ein zusätzlicher direkter Effekt von der UV1 auf die AV1 mit in die Modelldefinition aufgenommen wird. Der Rest der Syntax (außer dem Titel) bleibt dabei gleich, so dass hier nur der geänderte MODEL Abschnitt gezeigt wird:

MODEL:
med ON uv1 uv2;
av1 ON med uv1;
av2 ON med;
av1 WITH av2;
uv1 WITH uv2;

Wenn man dieses Modell schätzt, ergibt sich ein deutlicher besserer Fit (Output hier aus Platzgründen nicht abgedruckt): Chi-Quadrat-Test 37.347 bei 3 Freiheitsgraden ist noch signifikant, aber wesentlich niedriger als beim Ursprungsmodell. CFI ist gut mit .983, auch der SRMR mit .009. Der RMSEA ist weiterhin aufgrund der geringen Zahl Freiheitsgrade nicht interpretierbar, siehe oben.

6. Modellinterpretation (model interpretation)

Jetzt erst dürfen wir die Ergebnisse der Modellschätzung interpretieren. Interessant sind für uns vor allem die Regressionspfade sowie ggf. die Kovarianzen, so dass nachfolgend nur diese abgedruckt sind.

Unter MODEL RESULTS erhalten wir die unstandardisierten Schätzungen. Die Spalte Est./S.E. ist dabei die Teststatistik z.

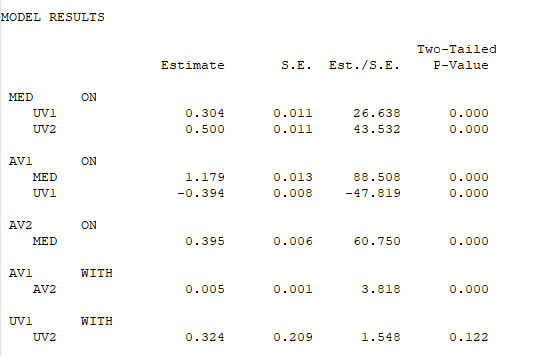
Darunter folgen die zusätzlich angeforderten standardisierten Schätzungen, die Interpretation der Spalten ist ansonsten vergleichbar.

Es schließt sich an die Angabe der erklärten Varianz der endogenen Variablen:

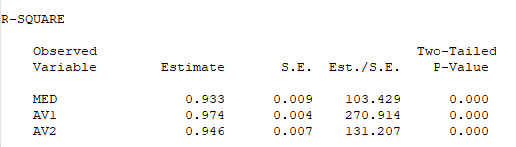
Schließlich folgen noch die zusätzlich angeforderten Konfidenzintervalle, zuerst die unstandardisierten und dann die standardisierten. Für ein zweiseitiges 95%-Konfidenzintervall benötigt man dann die Spalten „Lower 2.5%“ und „Upper 2.5%“.

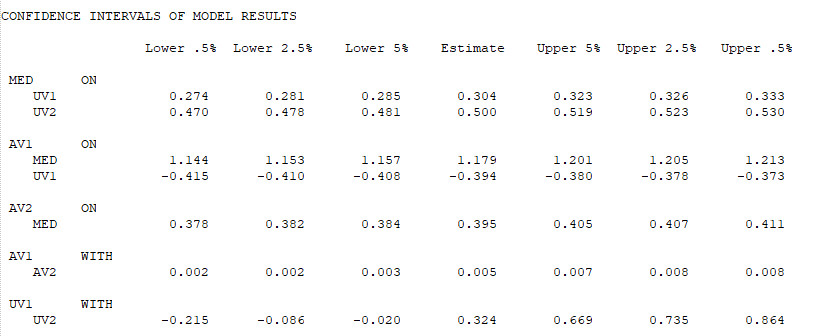
Die Ergebnisse kann man speichern (Menüpfad: File – Save As...) und man kann sich das Ergebnis der Modellschätzung auch visuell anzeigen lassen (Menüpfad: Diagramm – View diagram). Es öffnet sich dann ein neues Fenster mit dem Modelldiagramm. Über den Menüpunkt „View“ kann man auswählen, welche Informationen an die Pfeile geschrieben werden sollen. Und über den Menüpunkt „Diagram“ kann die optische Darstellung geändert werden; dabei ist es auch möglich, durch Anklicken und Verschieben die Lage der verschiedenen Kästchen in der Grafik zu ändern.

7. Quellen

Byrne, B. M. (2013). Structural equation modeling with Mplus: Basic concepts, applications, and programming. Routledge.

Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6(1), 1-55.